
Andrew Almond
After receiving a Physics degree from Edinburgh University in 1994, Andrew entered the School of Biological Sciences at University of Manchester. His Ph.D. thesis centered on the interaction of carbohydrates (especially hyaluronan) with water, both experimentally and theoretically. After obtaining his degree in 1997, he worked as a Wellcome Trust and BBSRC Research Fellow, designing joint theoretical and experimental approaches to study the dynamic conformation of hyaluronan, both free and in the presence of protein, and expanding his research into other polysaccharides and oligosaccharides. He is currently Lecturer in Biochemistry at the University of Manchester.

Timothy E. Hardingham
Tim majored in Biochemistry at the University of Bristol and received his Ph.D. there in 1968. He spent a large part of his career at the Kennedy Institute of Rheumatology in London (1968-1994), working with Helen Muir on proteoglycans and articular cartilage. This work identified hyaluronan as the key component in the aggregation of the cartilage proteoglycan aggrecan. Dr. Hardingham was awarded the Colworth Medal of the Biochemical Society (U.K.) in 1978. For his subsequent work on degenerative joint diseases, he was co-winner of the Roussel International Prize for Research on Osteoarthritis (1989) and the Carol Nachman Prize for Rheumatology (1991). He is now Professor of Biochemistry in the Wellcome Trust Centre for Cell-Matrix Research in the Faculty of Life Sciences, University of Manchester, and is investigating strategies for cartilage tissue engineering. He has continued research on the functions of proteoglycans and hyaluronan in the extracellular matrices.
The characteristic macro physical properties of hyaluronan (HA), which distinguish it from the other components of extracellular matrix, are readily accessible to experimentation and have been investigated and commented upon for over 50 years. However, a complete understanding of the microscopic shape of HA and how this translates into the macro physical properties has been much more elusive. In this article, we review new analysis of the macro physical behaviour and relate this to the latest evidence for the molecular interactions that govern HA behaviour at the local oligosaccharide level.
From its initial isolation, the properties of HA provided a challenge to classical biophysical methods of analysis, which were primarily developed for proteins and required that the properties approached those of perfect Newtonian solutes. The behaviour of HA in solutions even at low concentration is far from Newtonian, or “ideal”, and it required the talents of some very distinguished researchers; notably Sandy Ogston, Torvard Laurent, Endre (Bandi) Balazs and later Bob Cleland to make strong progress. Their work established a theoretical and experimental framework that provided a sound basis for beginning to understand HA’s distinctive properties1-3; and see: Hascall and Laurent Hyaluronan: Structure and Physical Properties and Laurent: The Tree: Hyaluronan Research in the 20th Century, in this series.
The key elements identified were:
Much of this early work was based on biophysical measurements of light scattering, osmometry, viscosity and sedimentation and this gave an evolving understanding of non-ideal behaviour and provided a basic structural model for HA that was consistent with results from the different techniques. However, it still appeared to leave the door open to various interpretations of what was the molecular detail of the conformation that caused the non-ideality.
Amongst the interpretations that have been put forward to explain HA behaviour was a model based on the self-association of HA chains in solution4. Although HA self-association might provide a possible explanation of some properties of HA, it was important to understand if it is compatible with all the experimental analysis of HA properties. Chain-chain self-association of HA would undoubtedly have a major and potentially dominant effect on its biophysical properties. For example, it might be hypothesised that if HA showed strong self-association in water it could cause it to be insoluble; secondly in dilute solution chain-chain association would be more likely to be intramolecular and would therefore tend to contract HA molecular domains and at high concentration when chain-chain association might also be intermolecular, it would form stable gels. The consequences of self association would vary depending on the strength and stability of the inter-chain bonds formed, but the known properties of HA (listed above) seem incompatible with the presence of strong chain-chain associations. However, it remained possible that weak transient interactions might be present and it was important to establish if there was any evidence of such interactions in aqueous solution of HA.
In the late 1990s, Hardingham and co-workers made a big step forward in the investigation of HA by developing a new approach to the analysis of its properties in solution. This approach was based on confocal-FRAP to determine the lateral translational diffusion of FITC-tagged HA in solution5-7 (Fig. 1). The technique is able to assess any factors that affected HA hydrodynamic behaviour, such as concentration, pH, ionic strength and temperature. Of particular importance for evaluating both strong and weak intermolecular interactions is that the technique is applicable to both dilute and concentrated solutions. It is also an equilibrium technique and is free of concentration gradients and moving boundaries, which can cause many artefacts in other biophysical measurements. The results could be interpreted based on empirical relationships8 established for the self-diffusion of polymers in good solvents and which reflect molecular entanglement of the polymer at high concentration. Further, the effects on the molecular domain of HA can be modelled using the Stokes-Einstein relationship to represent the hydrodynamic behaviour of HA as a sphere of equivalent dimension8. It was therefore ideal for investigating HA hydrodynamic behaviour and intermolecular interactions at equilibrium in free solution at both low and high concentration. It thus enabled us to provide a broad characterisation of the individual molecular properties of HA and the intermolecular interactions and network forming properties that occur when HA molecular domains become “crowded” and overlap as the concentration is increased. The latter was most important for the investigation of HA self-association, which might involve weak chain-chain interactions, as at high concentration chains would be closely spaced in solution and even weak interaction between chains would be more likely to be present. The confocal-FRAP technique was also suited to tracer diffusion measurements, which allowed an analysis of the way in which concentrated solutions of polymers impeded the diffusion of a soluble FITC-tagged tracer of smaller molecular size9. This enabled the apparent pore size of the “network” formed by the polymer in concentrated solution to be determined.
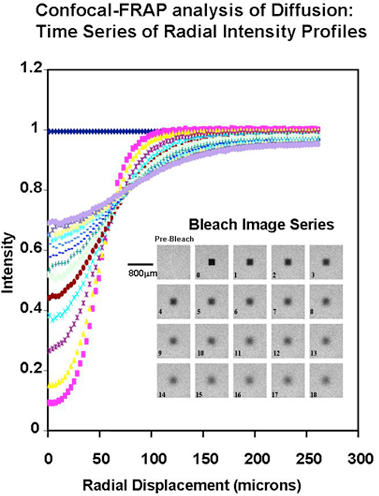
Fig. 1
Confocal-FRAP analysis of translational diffusion. Example of the confocal image set and the derived radial intensity profiles, for an experiment with FITC-dextran (260 kDa at 100 µg/ml in 0.1M NaCl at neutral pH and 25°C). The time zero image is 3 sec after the bleach and the interval between each subsequent image is 6 sec. (Further experimental details are in Ref. 5)
The initial determinations of the change in translational diffusion of HA as concentration was increased showed properties that were well described by solution entanglement (Fig. 2). This is a property common to all polymers in solution8. This implied that HA, as a polymer dissolved in a good solvent, such as water, behaved in a comparable manner to other polymers in good solvents and there was no evidence of intermolecular interactions at high concentration other than entanglement. The effect of ionic strength was also most informative, as it showed the great expansion of the hydrodynamic volume of HA as the ionic strength of the solution was decreased (Fig. 3, 4)10. This reflected the polyelectrolyte effect of charge repulsion of adjacent carboxyl groups along the HA chain causing expansion of the hydrodynamic domain. The results confirmed that HA was a polymer with a highly expanded hydrodynamic domain, which was entirely compatible with the long established model of a stiffened random coil. The properties in absolute terms were also molecular-weight dependent and confirmed that many of HA’s distinct properties are most noticeable because of its great chain length, including molecules up to 10,000 disaccharides long. The diffusional behaviour of HA showed little change across a broad range of pH 4-8. However, in strongly alkaline solution (pH 12-14) the hydrodynamic domain appeared to collapse, which suggested that whatever stiffens the chains is lost at high pH (Fig. 4) and under the conditions tested there was negligible depolymerisation of HA and the effect was reversed on lowering the pH 6. This effect of alkali is possibly caused by some hydroxyl groups on HA becoming ionised. Interestingly, it reduced the molecular domain to less than 1% of that in de-ionised water (Fig. 3) and the properties of HA became similar to those of a dextran of similar molecular weight. Investigation of the temperature dependence of HA self-diffusion gave unremarkable results and showed smooth minor changes in diffusion coefficient correlated with the change in viscosity of water with temperature. The result gave no evidence for a thermal melting of any intermolecular interaction of HA as might be predicted if there was chain-chain association. Evidence for chain-chain association was also absent in competition experiments with HA oligosaccharides. Self-association of HA molecules through chain-chain interaction would decrease their diffusion, whereas binding to short oligosaccharides would be unlikely to affect the rate of diffusion. In this case, the oligosaccharides should act as competitors of chain-chain interaction, but they had no effect on HA self-diffusion. The absence of any effect showed that HA hydrodynamic properties were unaffected by chain-chain competition9.
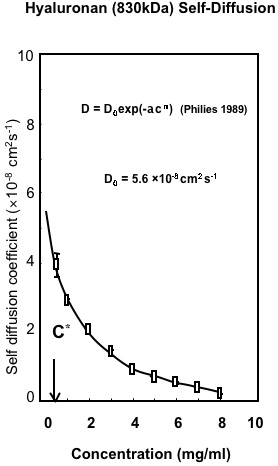
Fig. 2
Macroscopic Properties of Hyaluronan. Variation in the self-diffusion of HA with concentration determined by Confocal-FRAP. The results are fitted to the universal scaling equation proposed for polymers in solution8.

Fig. 3 HA (500 kDa)
The Effect of Salt and High pH on Hyaluronan Hydrodynamic Domain. Results represented as spherical domains based on the application of Stokes-Einstein relationship to the translational diffusion coefficients in dilute solution. D0 = κT/6πηRh where D0 is the diffusion coefficient at zero concentration, κ is Boltzmann痴 constant, T is temperature, η is solvent viscosity and Rh is the hydrodynamic radius.
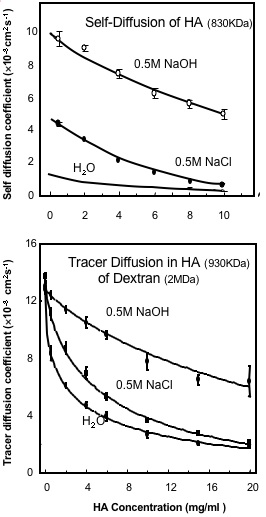
Fig. 4
The Effect of Salt and High pH on (A) the Translational Self-Diffusion Coefficient of Hyaluronan and (B) on the Tracer Diffusion of Dextran (2 MDa) in Hyauronan solutions6. The Hyaluronan is 830 kDa in (A) and 930 kDa in (B).
The analysis of tracer diffusion of FITC-labelled dextran (2 MDa) within concentrated solutions of HA (930 kDa and >1 mg/ml) showed a concentration dependent reduction in diffusion6, which could be modelled as an average pore size of 135 nm reducing to 30 nm as the concentration increased from 1mg/ml to 10 mg/ml. These properties were largely unchanged over a broad pH range (pH 4-8) and they showed only small changes with ionic strength6. This is because the concentration of chains is unaltered by ionic strength and therefore the chain density in solution, which is the main determinant of the reduction in diffusion of tracer molecules, is unchanged. It follows that although HA hydrodynamic domain increases and its self-diffusion decreases as the ionic strength is lowered, this would have no effect on the chain density in solution as long as the concentration remained above c* (the concentration at which the separate molecular domains begin to overlap). HA solutions at concentration below c* are inhomogeneous as they contain regions of high chain density within the molecular domains, but also regions with no chains between the molecular domains. The rate of tracer diffusion in an HA solution below c* will therefore be a time average of the free diffusion rate outside HA molecular domains and the reduced rate within the HA molecular domains. At concentrations below c* there will therefore be a more significant effect of ionic strength on tracer diffusion as the molecular domains expand at low ionic strength and contract at high ionic strength.
There will be physiological consequences if the concentration of HA in intercellular matrices fluctuates above and below c* and there are also likely to be further physiological effects caused by changes in the molecular weight of HA. If HA is depolymerised, this will reduce its molecular weight and its hydrodynamic domain. The concentration required for domain overlap, c*, will then be increased. So even without a change in concentration, depolymerisation can result in a switch from being above c* for high molecular weight HA, to being below c* for lower molecular weight HA, and this will result in increased rate of HA self diffusion and an increase in the rate of the diffusion of other macromolecules through the network. Depolymerisation of HA in tissues, even without a reduction in its concentration, will thus increase access through the ECM of macromolecules carrying signals to and from the cells.
Using the confocal-FRAP system for analysis of HA, there was only one condition under which there was some evidence of self association, and this was closely correlated with observations made many years ago. HA has previously been reported to form a viscoelastic “putty” if the solution is adjusted to pH 2.511. The effect is highly specific to this pH because at pH 3.0 and above, and at pH 2.0 and below, no similar effects were observed. In the confocal-FRAP analysis there was a sharp decrease in self-diffusion at pH 2.5, compared with pH 2.0 and 3.0. Interestingly this was accompanied by an increase in tracer diffusion in HA at pH 2.512. These two observations, lower self-diffusion and higher tracer diffusion are compatible with a model in which there is chain-chain association at this pH, as the association of chains could cause transient intermolecular links, which would lower self-diffusion. Further, the formation of sites of chain-chain association would create an uneven local distribution of chains, which would thereby create larger average pore sizes and thus an increase in tracer diffusion12. The molecular explanation of the HA putty formation at pH 2.5 is unknown, although it has been speculated that some effect of partial carboxyl group protonation at this pH may be involved. It is however most interesting as it shows that self-association was detected by confocal-FRAP with the consequences predicted. The unusual behaviour detected at pH 2.5 thus helps establish more securely that there is no similar chain-chain association at more physiological pH, nor at any ionic strength, nor at any concentrations of HA.
HA is thus a well-behaved large-molecular weight polymer, which in pure solution behaves as a stiffened random coil and has a highly expanded hydrodynamic domain that accounts for the formation of viscoelastic solutions determined by molecular entanglement10,12. These properties are compatible with the biological properties of HA, in which it can function as a large space filling, water commanding polymer as one of its functions, but also participates in a number of highly-selective interactions with proteins, whereby it can provide a polyvalent scaffold on which other bioactive molecules are assembled in multiple arrays.
Observations led those studying HA in the past to conclude that at the molecular level hyaluronan was not a totally unconstrained polymer. For instance, the polymer forms viscoelastic solutions at low concentrations that are not consistent with a freely flexible random coil, and secondly periodate oxidation of HA occurs more slowly than predicted13,14. However, much evidence also suggests that hyaluronan does not have a locally rigid structure. For example, hyaluronan is soluble up to very high concentrations, does not solidify, resists the formation of elastic gels and shows no evidence of chain-chain association9. Recent evidence from techniques such as confocal-FRAP (see above) backs up this view. How can we reconcile these two viewpoints? It is our hypothesis that these observations can be explained by a molecule that has an average local order in its 3D-structure, but with substantial dynamic flexing around this average structure. We will argue that this structural hypothesis is consistent with molecular dynamics (MD) calculations and with experimental data from nuclear magnetic resonance (NMR), and it also explains the bulk properties of HA and its physiological behaviour and function.
The first glimpse of the 3D molecular structure of HA came from x-ray scattering of orientated fibres in the 1970s15. Rather than observing a single, well-defined conformation, environmental factors (e.g., type of ion, level of hydration of the chains) resulted in dramatic changes to the observed diffraction pattern. By analysing the diffraction pattern from the fibres, the helical symmetry of the molecule can be determined and, in favourable cases, one can make a basic model for the 3D structure of the molecule. In the case of HA, left-handed helices were observed that have two-, three- and four-fold symmetry with a pitch between 0.8 and 1.0 nm (See Sheehan and Almond, Hyaluronan: Static, Hydrodynamic and Molecular Simulation views in this series)16. In the majority of cases the unit cells contained single chains in parallel, but under certain conditions two chains could be observed per unit cell in an anti-parallel arrangement, which led to a series of general observations. First, the shape of the unit cell could be profoundly affected by the type of ion present, and it was concluded that this may be due to solvent shells associated with different ions. Second, models that were consistent with x-ray diffraction often had the distinct possibility of intramolecular hydrogen bonds between sugar units. Third, not all of the fibre diffraction patterns could be used to construct viable models. For example, the two-fold x-ray diffraction pattern observed at low-pH was never fully-refined17. Therefore, refined structures produced from x-ray diffraction should be viewed with caution, not least because they are conducted under non-physiological conditions and may be an artefact of the crystallisation conditions.
An investigation of the literature shows that threefold and fourfold helices have been found under the largest range of conditions, and it is the fourfold helix that is found under arguably the most physiological conditions (the hydrated sodium ion)18. Based on these data, the most likely conformation in solution is a threefold or fourfold left-handed helix, involving intramolecular hydrogen bonds, which is supported by observations in solution (such as the slow rate of periodate oxidation and local rigidity of the HA chain concluded from hydrodynamic observations). Furthermore, the observation of multiple crystalline morphologies for HA suggests that it may be locally dynamic in solution, which is supported by the fact that HA maintains viscoelasticity up to high concentrations and does not form cuttable gels.
While x-ray diffraction studies provided major insight into the possible local conformations of HA, such studies are ultimately limited because they do not directly provide atomic-resolution information; the resolved image produced is static, and the relevance to understanding HA physiology is limited. One of the possibilities to overcome these limitations is to use modern computer methods, such as molecular dynamics (MD) simulations. Such methods attempt to describe the potential energy of the molecule through general empirical parameters that are calculated from theoretical (based on quantum mechanics) or experimental (spectroscopy) methods. Using these potential energies, local minimum energy 3D conformations can be calculated. However, realistic free energies can only be obtained by consideration of molecular entropy, which requires MD simulations that move the molecule over the potential energy surface. Furthermore, carbohydrates such as HA have a strong and molecular-level interaction with water, and this needs to be considered explicitly in order to understand, e.g., the dynamics of intramolecular hydrogen bonds. Such simulations, even for a HA tetrasaccharide require consideration of many thousands of atoms, are computationally very intensive, and thus have only been possible relatively recently.
Basic computer calculations show that the typical left-handed geometries found in the x-ray diffraction studies are consistent with the lowest energy conformations for the linkages19. In such a geometry, hydrogen bonds can be present at both linkages, which serve to lower the local energies and stabilise these structures. At both linkages, a hydrogen bond can be formed from a hydroxyl group (at OH3 or OH4 to the adjacent ring ether oxygen). In addition at the 1-4 linkage a (strained) hydrogen bond can be formed from the amide to the adjacent carboxyl moiety, while at the 1-3 linkage a hydrogen bond can be formed between the hydroxyl at position OH2 and the carbonyl oxygen. The resulting low-energy structure is consistent with left-handed threefold or fourfold helices, with a relatively contracted pitch per disaccharide (by comparison with x-ray diffraction studies). Such a structure can be used a basis for performing MD simulations in explicit aqueous solvent (Fig. 5).
When a computer model of a HA oligosaccharide is placed in a small droplet of water and heated to physiological temperatures, water molecules hydrogen bond to the surface of the HA molecule and break down intramolecular hydrogen bonds. In particular, for example, a water molecule coordinates itself between the amide and the carboxylate groups. The result of this, perhaps counter-intuitively, is that the molecule actually becomes more extended20. In these aqueous simulations, the local conformation was found to be on average approximately fourfold helix with the disaccharide as the fundamental unit21. Such a fourfold helix has an average disaccharide length of 0.96 nm (between next-but-one neighbouring glycosidic oxygen atoms) and an average axial rise of 0.84 nm (Fig. 6). This average structure can be downloaded from the protein data bank (http://www.rcsb.org/) using the code 2BVK22.
To quantify the dynamic structure further, it is useful to investigate the glycosidic linkages, which for convenience are defined here via the light (hydrogen) atoms. Thus the Φ-angle is defined as H1-C1-O-Cx and Ψ by C1-O-Cx-Hx; the other heavy-atom definitions can be found by adding or subtracting 120° (see below). Using this nomenclature, the average (Φ, Ψ) angles for the 1-3 linkage are (50.7°, 9.7°) and for the 1-4 linkage are (47.9°, 8.0°); both types of linkage are restricted to a relatively small region (standard deviation of ±13°) around (Φ, Ψ) = (50°, 10°).
The frequency of intramolecular hydrogen bonds can be monitored by a simple algorithm that considers each time step in the simulation and uses a filter to detect hydrogen bonds. A suitable filter corresponds to a distance between donor (D) and acceptor (A) electronegative atoms (which are either O or N in this case) of 0.35 nm and an angle (D-H-A) of greater than 120°. During simulations four intramolecular hydrogen bonds are seen per disaccharide and all are predicted to be in rapid (femtosecond timescale) exchange with solvent water molecules (spending less than 40% of the time in an intramolecular hydrogen bond), which leads to local chain flexibility (Fig. 7). The hydrogen bonds found are similar to those identified by x-ray fibre diffraction studies and basic molecular modelling (described above). To reiterate, at the 1-3 linkage OH2 donates to the carbonyl oxygen and OH4 to the adjacent ring oxygen, and at the 1-4 linkage the amine donates to a carboxylate-group oxygen, while OH3 donates to the adjacent ring oxygen.
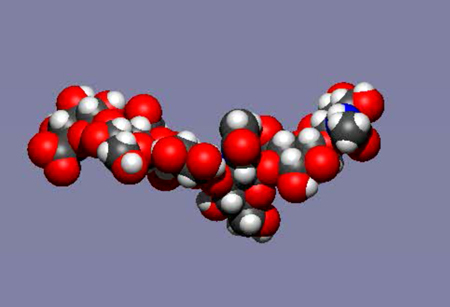
Fig. 5
TA mobile image of a molecular dynamics simulation of an HA hexasaccharide in water. Water has been removed from the image and the total real time elapsed is a few nanoseconds (the time taken for light to travel about 1 meter).See animation
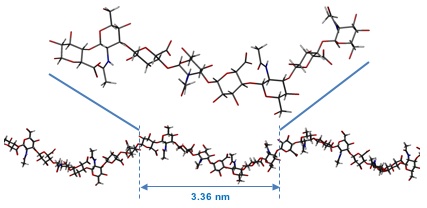
Fig. 6
The average predicted structure of an HA octasaccharide (top) from molecular dynamics simulations of HA in water. The overall shape of a longer fragment of HA derived from the local average structure. This fragment is longer than the persistence length and, while it represents the average structure, such a perfect structure would be predicted to occur only fleetingly in solution.
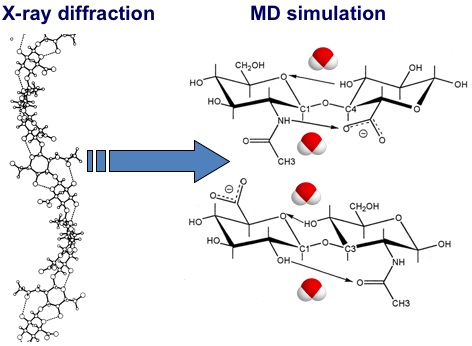
Fig. 7
Differences between the hydrogen bonds present in models of HA derived from X-ray diffraction studies in the solid state and from molecular dynamics simulations. In the static X-ray diffraction models the hydrogen bonds are omnipresent, while in molecular dynamics simulations all intramolecular hydrogen bonds are in competition with hydrogen bonds to water molecules. The exchange process is very quick (sub-nanosecond) and both intramolecular and water-bridged structures are present for significant proportions of the total time22, 25.
In the IUPAC nomenclature (used in the x-ray diffraction literature) the average predicted linkage dihedral angles are as follows: for the 1-3 linkage C1–O3–C3–C4 is 128.5°, O5–C1–O3–C3 is -68.1° and for the 1-4 linkage C1–O4–C4–C5 is -112.2° and O5–C1–O4–C4 is -71.1°. This average conformation is close to the orthorhombic antiparallel left-handed fourfold helical x-ray diffraction refinement that was obtained from fibres in the presence of sodium ions. The average axial rise per disaccharide predicted by the simulations (of approximately 0.84 nm) is consistent with these models, which are among the most contracted helices observed for HA in the solid state. Diffraction patterns obtained from potassium or calcium hyaluronate fibres are more extended than this average, which were refined as tetragonal and orthorhombic unit cells containing antiparallel left-handed threefold and fourfold helical chains with axial rises in the range 0.89-0.95 nm. Although the conformations derived from these diffraction patterns are not consistent with the average structure predicted by the simulations, they are well represented in the dynamic spread, as discussed previously. However, the extended twofold helices with an axial rise of 0.98 nm, proposed to be fundamental to the biological properties of HA, are only encountered transiently and are restricted to short sections of the HA chain extending over one or two disaccharides.
Specific testing of the computer models with 3D information from more physiological solutions of HA was achieved via NMR studies of isotopically enriched oligosaccharides. It was found that (as in proteins) the 15N-nucleus is very sensitive to its position in the oligosaccharide, and all amide groups could be individually assigned in oligosaccharides as long as decasaccharides, a major improvement on the previous best, a tetrasaccharide (a poor model for the polymer)23. By performing sensitive relaxation experiments at site-specific locations in oligosaccharides it was possible to estimate that the linkages explore a standard deviation of about 18° from the mean position, which is close to the 13° predicted by simulation24. Furthermore, site-specific measurement of NMR scalar couplings provide evidence of rotational mobility at the acetamido side-chain, from a trans (HN-N-C2-H2) mean orientation with a standard deviation of around 24°, close to the 18° inferred from simulations (Fig. 8). Specific NMR NOESY cross-peaks measured from each amide hydrogen to adjacent ring hydrogen atoms are also consistent with an acetamido group that is on average trans and a contracted HA local structure, rather than the extended twofold structure that has been proposed previously22.
Using these same labelled oligosaccharides, the amide proton chemical shift perturbation, carboxylate group pKa value, amide proton temperature coefficient and chemical exchange rates could be ascertained for every position in the oligosaccharide25. Such observations are found to be inconsistent with a highly populated hydrogen bond between the amide and carboxylate groups. Comparison of oligomer properties with polymeric HA indicates that there is no discernible difference in amide proton environment between the centre of octasaccharides and the polymer, again inconsistent with the formation of tertiary structures26. Therefore, the two key aspects of the secondary and tertiary structure models, which depend on highly populated intramolecular hydrogen bonds, are unlikely to be correct from the microscopic perspective.
These conclusions are mirrored by the simulations, which suggest that local dynamics of the amide groups are relatively unperturbed by the presence of a proximal carboxylate group and no evidence was found in the simulations for a strong, persistent hydrogen bond between amide and carboxylate groups across the 1-4 linkage. Instead, the two groups are predicted to be close to one another and interact via weak, transient hydrogen bonds that are rapidly interchanging with local water molecules (the strong interaction was present for only 4% of the time). This interpretation is in agreement with experimental observations described above, which suggest that if an intra-molecular hydrogen bond is present it cannot exist for more than 5-15% of the time.
These interactions maintain a conformation in HA oligosaccharides that is roughly fourfold in appearance, but with substantial local dynamics. The involvement of water molecules gives the linkage more flexibility, and can engender relatively large and rapid changes in conformation. Such an interpretation is in agreement with microscopic experiments from NMR and x-ray diffraction, and is also consistent with the hydrodynamic macroscopic behaviour of HA as a stiffened random coil in solution.
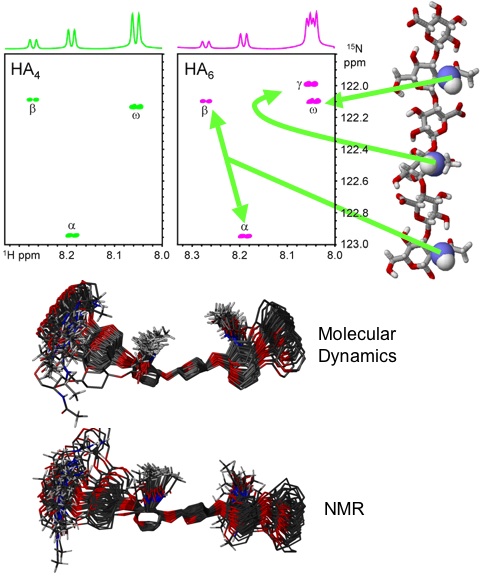
Fig. 8
1H-15N-HSQC NMR spectra of 15N-enriched tetra- and hexasaccharides from HA showing that all amide protons can be clearly resolved (top)23. An overlay based on the output from molecular dynamics simulations of a HA hexasaccharide in water is shown (middle) above the prediction based on measurements from NMR experiments of 15N-labelled HA oligosaccharides (bottom)22.
The unusual and distinctive properties of HA polymer solutions were established many years ago, but it is only more recently with the application new techniques that we are able to better define its molecular behaviour at the macroscopic polymer level and to quantify and model its behaviour at the local and atomic level. This has led to a much clearer understanding of how HA's distinguishing macro scale properties arise from the interaction of its local structure with the water and ions that surround it.