
Marta Pągielska
Master Student, Faculty of Chemistry, University of Gdańsk, Poland
Bioinformatician and data analyst, specializing in application of computational approaches to glycosaminoglycans within the project “Decrypting the ‘sulfation code’ of glycosaminoglycans for understanding their function in the extracellular matrix”. From 2022 a team member at Glycosaminoglycan Computational Group. Developer of a web-based database of cathepsin cysteine protease-glycosaminoglycan in silico interactions. Working on deciphering the sulfation code of glycosaminoglycans using state-of-art molecular modeling techniques, artificial intelligence algorithms and high performance computing to get novel insights into biologically relevant glycosaminoglycan-related molecular mechanisms.

Sergey A. Samsonov
Professor, Faculty of Chemistry, University of Gdańsk, Poland
After graduating in Biophysics in 2006 from the State Polytechnical University of St. Petersburg, he completed his PhD and did his postdoctoral research at Dresden University of Technology prior to obtain an independent position at the University of Gdańsk in 2017, where he is currently a leader of Glycosaminoglycan Computational Group (www.comp-gag.org). The group focuses on theoretical analysis of glycosaminoglycan containing biomolecular systems and development of novel computational approaches for them. The main techniques used in the group are molecular docking, all atomic and coarse-grained molecular dynamics as well as free energy calculations.
Glycosaminoglycans (GAGs), a particular class of linear anionic periodic polysaccharides, are key players in many biomolecular mechanisms underlying tissue regeneration and pathological processes such as cancer, Alzheimer’s and Parkinson’s diseases. They present significant challenges for experimental analysis due to their intrinsic physicochemical properties. That is why theoretical approaches to study these fascinating molecules are remarkably promising, especially in light of the immense increase in the computational resources available nowadays. In this article, we introduce you to the world of molecular modeling where you will learn about the basics of various techniques widely used in computational field, with a focus on GAGs research.
The human body has an incredible ability to heal wounds and regenerate tissues, which has intrigued scientists for centuries. Today, we can control some of these processes through medical treatments and have gained an understanding of the basic mechanisms, many involving glycosaminoglycans (GAGs). Unfortunately, what occurs deep within the molecules remains a mystery. Unlocking these secrets could revolutionize therapies for diseases and injuries, paving the way for more advanced regeneration techniques.

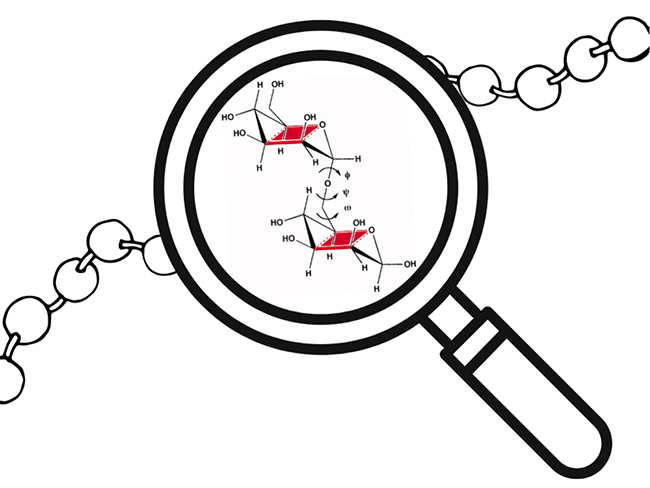
Sure, they’re carbohydrates! But what sets them apart is their flexibility and repeating structure. Chemically speaking, GAGs are a class of linear anionic polysaccharides consisting of repetitive disaccharide units. These building blocks are composed of uronic acid (glucuronic, GlcA, or iduronic, IdoA) and hexosamine (N-Acetylglucosamine, GlcNAc, or N-Acetylgalactosamine, GalNAc) (Figure 1). Disaccharide units are bonded via a covalent glycosidic linkage formed between the anomeric carbon of one sugar ring and a hydroxyl group of another sugar ring (Figure 2). The torsion angles φ (phi) and ψ (psi) define the three-dimensional conformation of this linkage, influencing the global flexibility of the polysaccharide chain.
GAGs can be sulfated in different positions. The amount (net sulfation) and particular positions of the sulfation group (sulfation pattern) constitute “sulfation code”, which determines GAG structure and biological function. This “sulfation code” is yet to be deciphered and lack of its understanding complicates studying GAGs due to its heterogeneity within a polysaccharide chain1. There are several types of GAGs, including chondroitin sulfate (CS), dermatan sulfate (DS), hyaluronic acid (HA), heparin/heparan sulfate (HP/HS) and keratan sulfate (KS). These types vary between each other depending on the specific type of uronic acid/hexosamine present and their distinct sulfation patterns, affecting their biochemical properties and interactions with other biomolecules. GAGs are found in the extracellular matrix and lysosomes of both vertebrates and invertebrates where they contribute to the structural integrity and biochemical environment. They are key players in various biological processes, from cell proliferation to angiogenesis and anticoagulation. Additionally, GAGs are involved in neurodegenerative diseases such as Alzheimer's and Parkinson's. Their role in these conditions is linked to their ability to interact with proteins, for example, influencing the aggregation, and so to participate in related pathologies. Studying GAGs may carry substantial impact on treatments of the aforementioned diseases.
Investigating GAGs experimentally poses significant challenges. X-ray crystallography requires static well-ordered samples (crystals) to produce clear diffraction patterns, but the flexible nature of GAGs often results in poor crystal quality and limited resolution. Consequently, this method is effective only for shorter GAGs. A more promising method to investigate the dynamic behaviour of GAGs could be Nuclear Magnetic Resonance. However, GAG repeating disaccharide units make it difficult to assign individual peaks to specific conformational states as those peaks may be overlapping. To overcome these experimental challenges, computational approaches alone or in combination with experiments have become essential, offering valuable insights into the structure and function of GAGs that are often inaccessible through experimental techniques exclusively2.
GAGs are highly charged, which means they mostly interact through electrostatic forces. So, calculating electrostatic potential of other molecules is key to understanding and predicting how GAGs interact with them. One effective way to visualize these electrostatic properties is through Electrostatic Potential (ESP) isosurfaces. The Poisson-Boltzmann Surface Area (PBSA) method is commonly used for calculating these surfaces. In PBSA, the solvent is treated implicitly meaning that the potential of mean force is applied to approximate the behaviour of many highly dynamic solvent molecules. Given the ESP isosurface, we are able to get insight into GAG potential binding regions and investigate them further with molecular docking approaches (Figure 3).
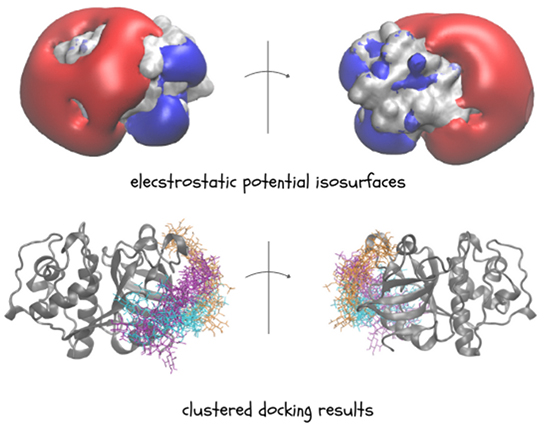
Knowing the potential binding regions, we can perform molecular docking. According to a definition, molecular docking is a computational technique used to predict the preferred orientation and binding affinity of a ligand when it binds to a protein forming a stable complex. The docking process typically involves the preparation of the ligand and receptor, docking simulation, pose scoring and ranking. Firstly, both the ligand (GAG) and the receptor (protein) are prepared, which includes adding hydrogens, assigning charges, optimizing their geometries and defining degrees of freedom affected through a docking run. The ligand is docked into the binding site of the receptor that can be done by various algorithms exploring different molecular orientations and conformations (docking poses). The scoring function evaluates each pose’s binding affinity based on how well the ligand fits into the binding site. Different poses are then ranked based on their scores and finally the best-scoring poses are analyzed further by structural clustering. Docking algorithms employ various scoring functions, including empirical, force field-, knowledge- and machine learning-based scoring methods3. Despite the variability of docking software, many do not perform satisfactorily for GAGs due to their flexibility and high charge. Programs such as AutoDock, Vina-Carb, and GlycoTorch Vina have been used but often struggle with accurate pose ranking. For example, Uciechowska et al. found that while AutoDock3 was the most successful, it still has limitations, such as the maximum number of considered torsional degrees of freedom, making it unsuitable for docking GAGs bigger than octamers4. The challenges come from the fact that even specialized docking software for carbohydrates often lacks appropriate scoring functions for GAGs. As a result, existing tools may not adequately capture the broad conformational space and complex interactions of longer GAGs.
For docking longer GAG chains we can use a special docking technique - fragment-based method. This approach involves breaking down a GAG into smaller, computationally manageable fragments such as trimers, which are docked individually to the protein surface. These fragments are then assembled into longer chains based on their overlaps, enabling the docking of GAGs without the length constraints of traditional methods. This technique is particularly useful for GAGs due to their repetitive structure, but it can struggle with binding near negatively charged regions.
In the context of receptor-ligand interactions, molecular docking results alone are not sufficient enough. Why? Because They only provide us a static structure. In such cases, Molecular Dynamics (MD) allows for the visualization of these molecules over time. This deterministic method enables the calculation of the trajectory of a system of molecules in phase space. It is based on the numerical solution of classical Newton's equations of motion.
To complement docking results, MD simulations are employed offering a dynamic view of GAG interactions (Figure 4)5. In all-atom MD simulations, every atom in a molecule is treated explicitly by a force field, which describes atomic types, bond lengths, angles, Lennard-Jones parameters, charges and the form of potential energy function defining the interactions between atoms. Most widely used force fields are CHARMM, AMBER, and GROMOS offering high-resolution structural insights. This approach can be compared to a "ball-and-spring" model, where atoms are represented as balls and the bonds between them are modeled as springs. This detailed representation allows for precise modeling of GAGs, capturing their intricate conformational changes and interactions at the atomic level.
To investigate GAGs in larger spatial and temporal scale we need to shift into lower resolution offered by coarse-grained (CG) modeling. In this approach, groups of atoms are treated as single pseudoatoms, simplifying the system and significantly enhancing computational efficiency. CG force fields can be classified into empirical, physics- or machine-learning-based, each offering different levels of accuracy and computational efficiency for simulating GAGs6. Despite the presence of CG force fields for carbohydrates, they are often not applicable for GAGs. For example, empirical MARTINI force field requires restraints on protein structures while simulating protein-GAG complexes. On contrary, the physics-based carbohydrate SUGRES-1P force field, which has recently been extended to heparin, is more promising7. In this model, each sugar residue in the polysaccharide chain is represented by a single interaction site positioned midway between the glycosidic linkage oxygen atoms acting as the anchor points for the whole chain.
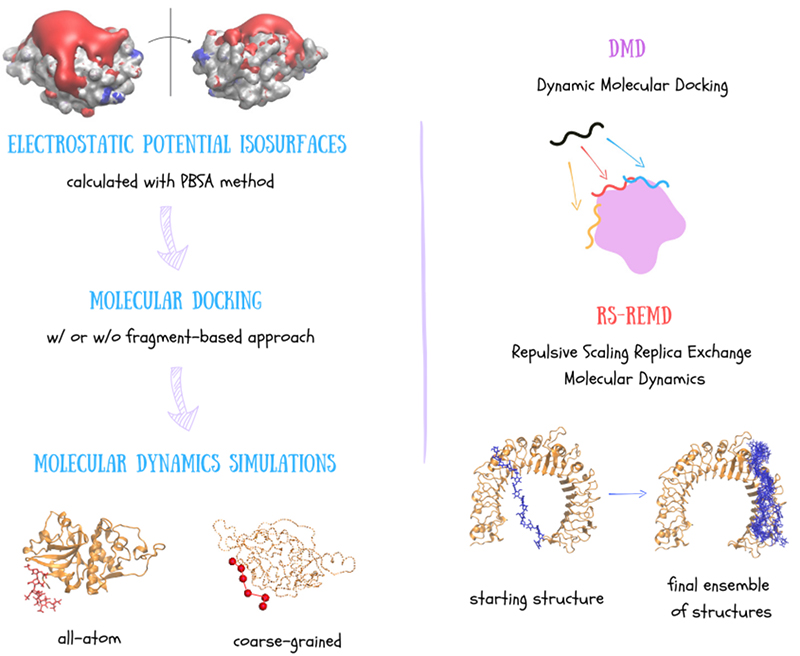
Well, for longer GAG chains, classical docking methods really fall short! So, we might as well skip them8. Instead, effective method may be Dynamic Molecular Docking (DMD), which is a combination of molecular docking and molecular dynamics. DMD applies an additional potential to guide the GAG from a distant position towards the binding site on the receptor's surface9. While this method can be effective, it requires prior knowledge of the binding site and can be computationally expensive due to large initial distance between the receptor and the ligand.
Another docking approach, Repulsive Scaling Replica Exchange Molecular Dynamics (RS-REMD) turns out to be tremendously valuable for GAGs10. RS-REMD improves sampling efficiency by running multiple simulations (replicas), where the atomic radius and Lennard-Jones parameters are adjusted, periodically exchanging configurations between them. This method helps the system overcome energy barriers and avoid local minima, ensuring a more thorough exploration of the conformational space. RS-REMD has been successfully adapted for protein-GAG systems and tested for GAG of various lengths, showing promising results in identifying binding sites and poses. Despite its high quality performance, RS-REMD may face challenges in predicting binding within confined protein pockets or distinguishing GAG binding poses of opposite orientations.
Let’s dive into this! Accurate calculation of binding free energy is crucial for understanding GAG interactions with other molecules. We can use a bunch of methods to get the scoop on how stable and dynamic receptor-ligand complexes are (Figure 5).
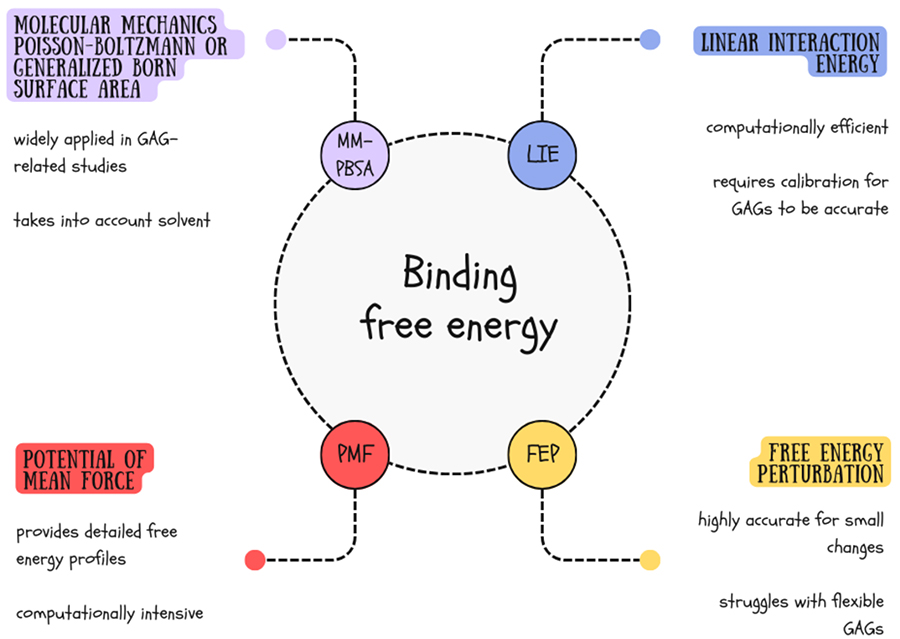
MM-PBSA (Molecular Mechanics Poisson Boltzmann Surface Area) and its approximation MM-GBSA (Molecular Mechanics Generalized Born Surface Area) are the most popular methods for calculating binding free energy for GAG containing systems11. In these approaches, we calculate the sum of the non-bonded interaction energy ("gas phase energy"), consisting of electrostatic and Lennard-Jones interaction energies, the free solvation energy and the entropic contribution from MD trajectories.
Another even quicker method for calculating binding affinity at the endpoints is LIE (Linear Interaction Energy). It originates from the Linear Response Approximation (LRA) method and was proposed in 1994 by Åqvist and colleagues12. The main assumption of the method is that only the time-averaged interaction energies between the ligand and its surroundings are considered to obtain an estimated binding free energy. Binding free energy in LIE is proportional to the weighted sum of the electrostatic and van der Waals interaction energies, accounting for both the bound and unbound states of the ligand. Despite being simple and straightforward LIE may be even more accurate than MM-GBSA when calibrated for a representative dataset containing molecules of the same type.
For more detailed insights into the energy landscape of binding processes, the Potential of Mean Force (PMF) method is often used. PMF calculates free energy profiles along a reaction coordinate, providing detailed information about free energy barriers and intermediates along the binding or reaction pathway. This method offers a comprehensive view of complex interactions, though it requires extensive sampling and is computationally expensive. It also requires careful selection of reaction coordinates to avoid misleading energy profiles.
Lastly, the Free Energy Perturbation (FEP) method stands out for its high accuracy in calculating free energy differences between two states. By sampling intermediate states, FEP is particularly effective for studying small perturbations, such as mutations or minor ligand modifications. Despite its precision, FEP is computationally demanding and requires careful convergence checks to ensure reliable results13. Therefore, it works well for rigid structures, becoming less useful for such flexible molecules as GAGs.
Yes, it is! Water plays a crucial role in stabilizing protein-GAG complexes, maintaining proper interactions and mediating a significant number of protein-GAG contacts. Various water models are employed to simulate these interactions, with implicit and explicit being the primary types. Implicit one approximate solvent effects as a continuous medium, which reduces computational complexity and speeds up simulations. While less accurate than explicit models, they are valuable for large systems due to their efficiency. However, they can overestimate salt bridge strength and deviate in secondary structure predictions. Therefore, explicit water models, in which a water molecule is represented with individual particles explicitly, offer a more accurate description of solvent interactions. They vary in terms of flexibility, number of interaction sites and polarizability. Common examples include TIP3P, TIP4P and TIP5P, which are rigid 3-, 4- and 5-center models, respectively. The TIP3P model, despite its lower accuracy compared to more complex models like TIP4P or TIP5P, is more often employed in GAG-related studies due to its low computational cost. It effectively supports simulations by maintaining the structure of protein-GAG complexes and properly capturing hydration effects14,15.
With all sorts of molecules, from ions to big proteins (Figure 6)! GAGs interact extensively with divalent cations due to their highly negatively charged nature. This charge density allows GAGs to form ionic bonds with positively charged ions such as calcium (Ca2+), magnesium (Mg2+), zinc (Zn2+), manganese (Mn2+) etc. These interactions are crucial for the structural stability of GAGs as well as their biological functions. For example, calcium ions can stabilize the GAG structure by bridging sulfate and carboxylate groups16, which is important for their role in cartilage, connective tissues, and other biological processes.

GAGs also form complexes with small molecules. Their highly flexible periodic structure and negative charge enable them to bind short therapeutic peptides, inhibitors or bioactive compounds becoming invaluable in drug design17. In this context, GAGs can act as carriers or reservoirs, slowly releasing bound drugs to maintain therapeutic concentrations over time. When it comes to larger biomolecules, GAGs interact extensively with a wide range of proteins, such as growth factors, chemokines and cathepsins1. These interactions are also mainly driven by electrostatic forces, given the negative charge of GAGs and the positively charged regions of proteins. For instance, GAGs can bind to growth factors such as fibroblast growth factor (FGF) or transforming growth factor-beta (TGF-β), influencing their ability to activate signaling pathways, which in turn regulates cellular responses like proliferation or differentiation. Similarly, GAG interactions with chemokines play a pivotal role in immune cell recruitment and inflammation.
– GAGs represent a particular class of linear anionic periodic polysaccharides that are key players in many biomolecular mechanisms (e.g. tissue reparation, cell signaling, pathological processes).
– GAGs may be challenging for the experimental analysis due to their negative charge, flexibility and periodicity.
– Computational approaches, such as molecular docking, molecular dynamics and free energy calculations, have become invaluable for studying GAGs.
– The in silico protocols allow for structural predictions, description of the dynamic behaviour of the systems and estimation of the binding affinity.
– Use of GAG-specific computational approaches alone or combined with experimental techniques could significantly enhance our understanding and facilitate application of GAGs in regenerative medicine and drug development.