
氏名:マルタ・ポギエルスカ
ポーランド グダニスク大学 化学系 修士課程
専門はバイオインフォマティクスおよびデータ解析。プロジェクト「細胞外マトリックスにおけるグリコサミノグリカンの機能理解のための硫酸化コードの解読」において計算化学の適用を担当している。2022年よりサムソノフ教授の研究室メンバー。システインプロテアーゼであるカテプシンとグリコサミノグリカンのin silico相互作用に関するWebベースデータベースの開発者でもある。現在、最先端の分子モデリング技術、人工知能アルゴリズム、および高性能コンピューティングを駆使してグリコサミノグリカンの硫酸化コードの解読に取り組んでいる。グリコサミノグリカンが関連する生物的分子メカニズムの新たな洞察に尽力している。

氏名:セルゲイ・サムソノフ
ポーランド グダニスク大学 化学系 教授
2006年にロシアのサンクトペテルブルク国立工科大学にて生物物理学の学位を取得。その後、ドイツのドレスデン工科大学において博士課程を修了し、同大学にて博士研究員の勤務の後、2017年にポーランドのグダニスク大学で独立したグリコサミノグリカン計算グループ (www.comp-gag.org)を設立し、そのリーダーを務めている。同グループは、グリコサミノグリカンを含む生体分子システムの理論的な分析と新しい計算手法の開発に重点を置いている。グループで使用される主な手法は、分子ドッキング、全原子および粗視化分子動力学、自由エネルギー計算などである。
グリコサミノグリカン(略称GAG)は直鎖状の多糖の一種で、組織の再生や、ガン、アルツハイマー病、パーキンソン病をはじめとする様々な病理学上の生体プロセスに関与している。しかしながら、化学実験を通してGAGの性質を見極めていくことは物理化学的性質上困難である。ここに理論化学計算を適用することのメリットが存在する。特に、計算機性能が著しく向上した近年においては、その傾向がより顕著となってきている。本稿においては、GAGを計算対象とした分子モデリングの世界をご紹介しなら、計算機化学の様々な手法についても理解を深めて頂ければと考える。
ヒトの身体は、傷を癒やし、組織を再生する驚異的な能力を有している。この能力は長年多くの研究者を魅了してきたが、これらのプロセスの一部は医療行為を通じてコントロールすることが今や可能となってきており、その基本的なメカニズムへの理解も深まってきている。またそのプロセスの多くにGAGが関与していることも明らかにされつつある。しかしながら分子内で実際に何が起きているのかまではまだまだ我々の理解が及んでいない。これらの秘密を解き明かしていくことが、病気や傷の治療やひいては新たな再生医療へと繋がるものと期待されている。
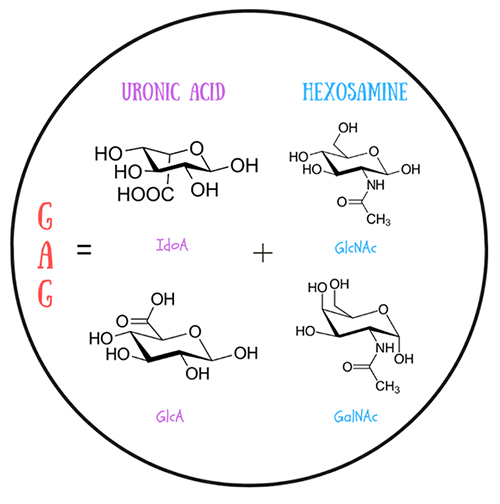
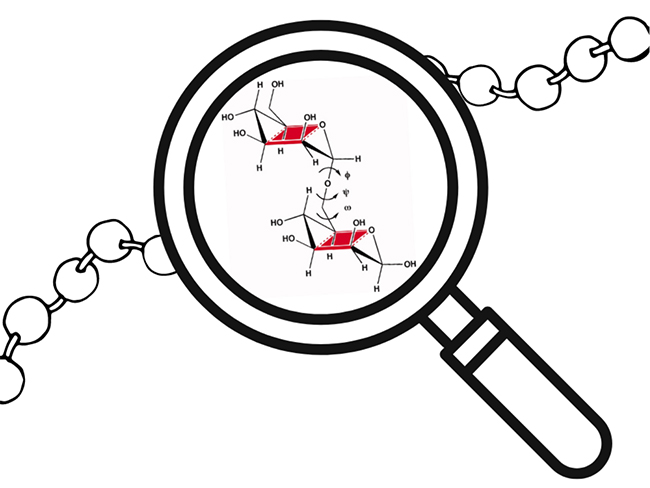
GAGはその名が示す通り多糖類であるが、その大きな特色は繰り返し構造とその組み合わせの柔軟性にある。化学的な定義に基づけば、GAGは二糖類を基本単位とした繰り返し構造からなる直鎖状のアニオンの多糖類の一種と位置付けられる。その構成要素は、ウロン酸(グルクロン酸、GlcA またはイズロン酸、IdoA)とヘキソサミン(N-アセチルグルコサミン、GlcNAc または N-アセチルガラクトサミン、GalNAc)である(図 1)。二糖類は、1つの糖環のアノマー炭素と別の糖環のヒドロキシル基の間に形成される共有グリコシド結合を介して結合している(図 2)。ねじれ角 φと ψは、このネットワークの3 次元構造を決定し、多糖鎖全体の柔軟性に影響を与えている。
GAGはさまざまな位置に硫酸化修飾を施すことが可能である。硫酸基の位置とその量はいわゆる「硫酸化コード」を構成し、GAGの構造とその生物学的機能を決定づける。この「硫酸化コード」はいまだ完全には解読されておらず、その理解不足と多糖鎖内の不均一性がGAGの研究を複雑にしている1。GAGには、コンドロイチン硫酸(CS)、デルマタン硫酸(DS)、ヒアルロン酸(HA)、ヘパリン/ヘパラン硫酸(HP/HS)、ケラタン硫酸(KS)などいくつかの種類が存在する。これらは、その中に存在するウロン酸/ヘキソサミンの種類や、それらの硫酸化パターンが互いに異なっており、その違いが生化学的特性や他の生体分子との相互作用に影響を及ぼす。GAGは、脊椎動物と無脊椎動物の双方の細胞外マトリックスとリソソームに存在し、構造的完全性と生化学的環境に寄与している。これらは、細胞増殖から血管新生、抗凝固まで、さまざまな生物学的プロセスで重要な役割を果たしている。さらに、GAGはアルツハイマー病やパーキンソン病などの神経変性疾患にも関与している。これらの疾患におけるGAGの役割は、たとえばタンパク質と作用する能力、凝集に影響を与える能力、および関連する病理に関与する能力にも関連している。それゆえGAGの研究は、前述の疾患の治療の進展に大きく寄与する可能性をも秘めている。
GAGの構造の実験的な同定には様々な課題が残されている。まずX線結晶構造解析を用いる場合、明確な回折パターンを生成するためには静的で規則正しく並んだ構造(結晶)が必要だが、GAGは柔軟な構造を持つため結晶構造が乱れ、解像度が制約されることがよくある。そのため、この手法は長さの短いGAGにしか有効でない。GAGの動的挙動を調べるためのより有望な方法は核磁気共鳴法(NMR)であるが、GAGが二糖単位の繰り返し構造である性質上NMRのピークが重なりあう場合が多く、個々のピークを特定の立体配座状態に割り当てる作業は容易ではない。これらの実験上の課題を克服するために、計算的手法あるいは計算と実験の組み合わせが不可欠となる。計算的手法を採り入れることで、実験手法だけでは得られないGAGの構造と機能に関する貴重な洞察が得られる場合が多い2。
GAGは分子全体が高い電荷を帯びており、主に静電力による相互作用に関与する。したがって、分子の静電ポテンシャルを計算することは、GAGがその分子とどのように相互作用するかを予測する鍵となる。静電特性を視覚化する効果的な方法の1つは、静電ポテンシャルマップ(ESP)を使用することである。そのポテンシャル表面を計算するために一般的に利用されるのは、ポアソン・ボルツマン表面積法(PBSA)である。PBSA法においては、溶媒は「陰溶媒」として扱われる。すなわち、溶媒は個々の溶媒分子として直接扱われるのでなく、平均力のポテンシャルが適用され、多くの動的な溶媒分子の挙動が近似される。ESP等値面が与えられれば、GAGの潜在的な結合領域についての洞察が得られ、分子ドッキング手法でさらに詳しく調べることが可能となる(図 3)。
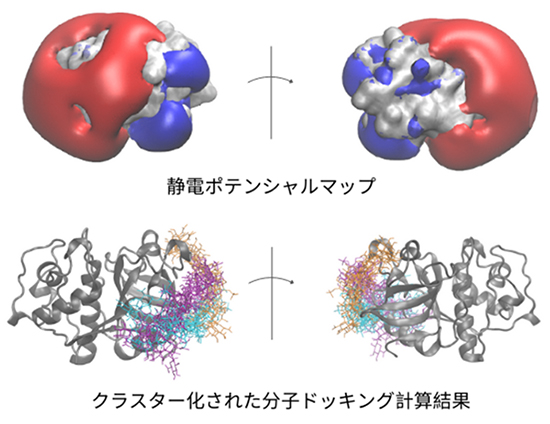
結合領域のおおよその目処がつく場合は分子ドッキングが実行可能である。分子ドッキングとは、「リガンドがタンパク質に結合して安定した複合体を形成する際の、リガンドの優先配向と結合親和性を予測するために使用される計算手法」である。分子ドッキングの進め方は、(1)リガンドと受容体の分子構造の準備、(2)実際のドッキングシミュレーション、(3)ポーズのスコアリング(点数付)とランク付け、の3部構成からなるのが通常である。それにはまず、リガンド(ここではGAG)と受容体(タンパク質)の分子構造ファイルが必要とされる。これには(結晶構造には欠けている)水素原子の追加、電荷の割り当て、形状の最適化、ドッキング実行によって影響を受ける自由度の定義なども含まれる。リガンドは受容体の結合部位にドッキングされるが、さまざまなアルゴリズムを通して探索可能であり、多様な分子配向と立体配座(ドッキングポーズ)を探索することが可能である。スコアリング関数は、リガンドが結合部位にどれだけ適合するかに基づいて、各ポーズの結合親和性を評価する。次に、様々なポーズがスコアに基づいてランク付けされ、最後に最もスコアの高いポーズが構造クラスタリングによって分析される。ドッキングアルゴリズムはさまざまなスコアリング関数を採用しており、それには経験的、力場、知識、機械学習に基づくスコアリング方法が含まれる3。ドッキングソフトウェアの多様性にもかかわらず、その多くはGAGに対してその構造の極度な柔軟性と高電荷のために満足のいく結果を示せていない。例えば、AutoDock、Vina-Carb、GlycoTorch Vinaなどのプログラムが一般に知られているが、正確なポーズのランク付けに苦労することが多々見られる。Uciechowskaらは、AutoDock3が最も分子ドッキングに適していると結論づけたものの、プログラムで考慮されるねじれ自由度の最大数などの制限があり、八量体よりも大きいGAGのドッキングには適していないとも結論づけている4。課題は、炭水化物専用のドッキングソフトウェアでさえも、GAGの適切なスコアリング関数を欠いていることが多いという点に象徴される。その結果、既存のツールでは、長いGAGの広いコンフォメーション空間と複雑な相互作用を適切に捉えられないリスクがある。
受容体とリガンドの相互作用を調べる目的の場合、分子ドッキングの計算のみでは不十分である。なぜならこの手法を用いただけでは静的な構造しか得られないからである。その場合、分子動力学計算(MD)を使用すると、これらの分子を時間の経過とともに視覚化することができる。この決定論的方法により、位相空間における分子システムの軌跡を計算することができる。MD計算は古典的なニュートンの運動方程式の数値解に基づいている。
ドッキング計算結果に加えて、MD計算を用いてGAGと分子の相互作用の動的イメージを補完する場合がしばしばある(図 4)5。全原子型のMD計算では、分子内のすべての原子が力場によって明示的に処理され、原子タイプ、結合長、角度、Lennard-Jonesパラメーター、電荷、および原子間の相互作用を定義するポテンシャルエネルギー関数の形式が記述される。最も広範に使用されている力場は、高解像度の構造的洞察を提供することができるCHARMM、AMBER、およびGROMOSである。この手法では、原子がボールとして表され、それらの間の結合がバネとしてモデル化される「ボールとバネ」モデルに例えることができる。このように分子を厳密に再現する手法により、GAGの正確なモデル化が可能となり、原子レベルでの複雑な構造変化と相互作用を捉えることができる。
GAG をより広い空間および時間スケールで調べるには高解像度のMD計算では計算機資源に限界があり、粗視化(CG)モデリングによる低解像度の計算に移行する必要が出てくる。CGモデルでは、原子集団を一つの擬似原子として扱うため、システムが簡素化され計算効率が大幅に向上される。CG 力場は、経験的、物理ベース、機械学習ベースに分類され、それぞれが異なるレベルの精度と計算効率を提供している6。炭水化物用の CG 力場は実際に存在するものの、GAG には適用できない場合がある。たとえば、経験的な MARTINI 力場では、タンパク質-GAG 複合体をシミュレートする際にタンパク質構造に制約が必要となる。それとは対照的に、最近ヘパリンにも拡張された物理ベースの炭水化物 SUGRES-1P 力場はGAGへの応用が有望視されている7。このモデルでは、多糖鎖内の各糖残基は、糖鎖全体のアンカーポイントとして機能するグリコシド結合酸素原子の中間に位置する単一の相互作用部位によって置き換えられることとなる。
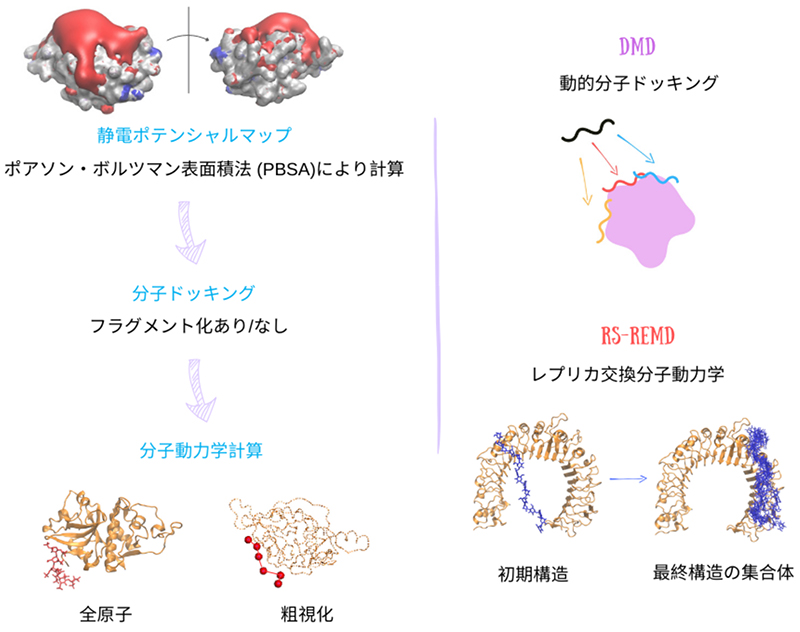
長いGAG鎖の場合、古典的なドッキング法では不十分な場合が多い。このような手法はそもそもGAGの計算に適さないとも言える8。代わりに、分子ドッキングと分子動力学を組み合わせた動的分子ドッキング(DMD)が効果的な場合がある。DMD法では、GAGを受容体の離れた位置からその表面の結合部位に向かって誘導するための追加のポテンシャルを導入している9。DMD法は効果的な手法ではあるものの、結合部位に関する事前情報が必要とされ、受容体とリガンド間の初期距離が大きいため計算コストが高くなる傾向がある。
もう 1 つのドッキング手法である反発スケーリングによるレプリカ交換分子動力学(RS-REMD)は、GAG の計算に極めて有望であることが明らかになりつつある10。RS-REMD では、原子半径と Lennard-Jones パラメータを調整し、それらの構成を随時交換するシミュレーションを複数実行する(レプリカと呼ばれる)ことで、サンプリング効率を改善する。この方法は、エネルギー障壁の克服、局所最小値の回避、コンフォメーション空間の探索において威力を発揮する。RS-REMDは、タンパク質-GAG システムにうまく適応され、さまざまな長さの GAG を用いてテストされ、結合部位とポーズの識別で有望な結果を示している。その高いパフォーマンスにもかかわらず、RS-REMD には、タンパク質の結合ポケット内での結合の予測や、GAG 結合ポーズの配座の区別などの課題が残されている。
正確に結合自由エネルギーを計算できることは、GAG と他の分子との相互作用を理解するために不可欠なツールとなる。受容体とリガンドの複合体の安定性と動的性について詳しく知るには、さまざまな手法が適用可能である(図 5)。
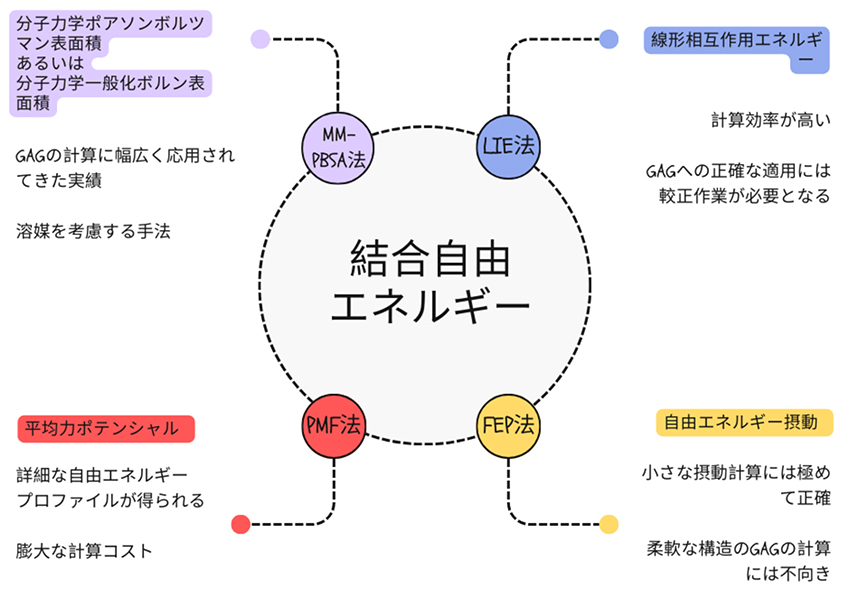
MM-PBSA法(分子力学ポアソンボルツマン表面積)とその近似法であるMM-GBSA法(分子力学一般化ボルン表面積)は、GAG含有システムの結合自由エネルギーを計算する最も一般的な手法として知られている11。これらの手法では非結合相互作用エネルギー(いわゆる「気相エネルギー」に相当)の累計が計算されるが、その内訳は静電相互作用エネルギー、Lennard-Jones相互作用エネルギー、自由溶媒和エネルギー、およびMD軌道からのエントロピー寄与により構成される。
結合親和性を計算するより高速な手法としてLIE 法(線形相互作用エネルギー)が知られている。これは線形応答近似法(LRA)に由来し、1994 年に Åqvistらによって提案された12。LIE 法では、結合自由エネルギーの計算において、リガンドとその周囲との間の時間平均化された相互作用エネルギーのみを用いる特徴がある。LIE 法に基づく結合自由エネルギーは、ウエイトを加えた静電相互作用エネルギーとファンデルワールス相互作用エネルギーの合計に比例しており、これにはリガンドの結合状態と非結合状態の双方が考慮されている。極めてシンプルな手法であるにも関わらず、LIE 法は同じタイプの分子を含むデータを用いて較正を行った場合、MM-GBSA よりも正確なエネルギーを得られる可能性を秘めている。
結合プロセスの俯瞰エネルギー分析を詳細に行うには、平均力ポテンシャル法(PMF)がよく用いられる。PMF法では、反応座標に沿って自由エネルギープロファイルを計算し、結合または反応経路に沿った自由エネルギー障壁と中間体に関する詳細な情報が得られる。この方法では、複雑な相互作用を包括的に把握することができるが、広範なサンプリングが必要とされる手法であるため、計算コストが膨大になる傾向がある。また、誤ったエネルギープロファイルに仕上がるのを避けるためには、反応座標を慎重に選択する必要があることにも留意する必要がある。
最後に紹介する自由エネルギー摂動法(FEP)は、2つの異なる状態間の自由エネルギー差を計算する際に高い精度を発揮する。中間状態にある分子をサンプリングすることで、FEP法は突然変異やリガンドの軽微な変異などの小さな摂動を研究するのに特に効果的な手法である。FEP法は精度が高い手法ではあるものの、必要とされる計算量が膨大で、さらに信頼性の高い結果を担保するためには計算の収束状況を随時慎重に確認することが求められる13。このため、構造に揺らぎの少ない分子の計算には有効であるものの、GAGのような柔軟な分子には適していないとも言える。
水分子は、タンパク質-GAGの接触を媒介することで、その複合体を安定化するのに重要な役割を果たしている。こうした相互作用をシミュレートするためにさまざまな水分子のモデルが用いられているが、これらは「陰溶媒」あるいは「陽溶媒」としてモデルする2つの手法に大別される。陰溶媒としてモデルする場合は、溶媒効果を連続溶媒として近似するため計算が大幅に簡素化され、シミュレーションが高速化される。個々の溶媒分子を露わに扱う手法(陽溶媒)に比べて正確性では劣るものの、計算効率が高いため大規模システムで有効な手法である。ただし、塩橋(残基間の相互作用)の強度を過大評価する傾向があるほか、タンパク質の二次構造の予測に失敗するケースもある。他方、水分子を個々の粒子で明示的に扱う明示的水モデル(陽溶媒)では、溶媒相互作用をより正確に記述できる。陽溶媒として扱う場合においても、柔軟性、相互作用部位の数、分極率の点で異なるモデルがいくつか存在する。広く一般的に使われるモデルとしては、それぞれ 3、4、5 中心の剛体モデルである TIP3P、TIP4P、TIP5P がある。 TIP3Pモデルは、TIP4PやTIP5Pのようなより複雑なモデルに比べて精度はやや劣るものの、計算コストが低いためにGAG関連の研究では幅広く採用されている。こうした水分子モデルを用いることで、タンパク質-GAG複合体の構造が適切に保持され、水和効果も適切に再現することによって、分子シミュレーションの正確性が担保させている14,15。
GAGはイオンのような小分子から巨大なタンパク質に至るまで、あらゆる分子と相互作用する(図 6)。GAGは高い負電荷を有するため、様々な2価カチオンと相互作用を行うが、その電荷密度の高さにより、カルシウム(Ca2+)、マグネシウム(Mg2+)、亜鉛(Zn2+)、マンガン(Mn2+)などの正電荷を帯びたイオンとイオン結合を形成する。こうした相互作用は、GAGの構造安定性と生物学的機能にとって重要となる。たとえば、カルシウムイオンは硫酸基とカルボキシル基を架橋することでGAGの構造を安定化できる16。これは、軟骨、結合組織、およびその他の生物学的プロセスで重要な役割を担うこととなる。
GAG はイオン以外の小分子と複合体を形成する。その柔軟な周期構造と負電荷により、治療用の短いペプチド、阻害剤、あるいは生理活性化合物とも結合することができ、医薬品設計において極めて有用な存在となっている17。この場合、GAG は薬剤を運搬そして保管する機能を有し、結合した薬剤をゆっくりと時間をかけて放出しながら治療濃度を維持する。さらに大きな生体分子について言えば、GAG は成長因子、ケモカイン、カテプシンなどの幅広いタンパク質とも広範囲に相互作用する1。これらの相互作用も、主にGAG の負電荷とタンパク質の正電荷領域による静電気力によって引き起こされている。たとえば、GAG は線維芽細胞増殖因子(FGF)や形質転換増殖因子ベータ(TGF-β)などの成長因子と結合し、シグナル伝達経路を活性化する能力に影響を与え、それが増殖や分化などの細胞応答を制御する。同様に、GAG とケモカインの相互作用は、免疫細胞の動員と炎症において極めて重要な役割を果たしている。
GAG 分子とは、多くの生体分子メカニズム(組織修復、細胞シグナル伝達、病理学的プロセスなど)において重要な役割を果たす、特定のクラスの線状アニオン性周期性多糖類である。
GAG は、その負電荷、柔軟性、周期性のため、実験的に分析することが困難な場合が多い。
分子ドッキング、分子動力学、自由エネルギー計算をはじめとする計算的な手法は、GAG の機能を理解するのに非常に重要な手法となっている。
計算機を使用したいわゆるin silicoな手法に基づいて、構造予測、システムの動的動作の説明、結合親和性の推定が可能となる。
GAG に固有な計算手法を、単独あるいは実験手法と組み合わせて使用することで、再生医療や医薬品開発における GAG の理解を大いに深め、GAGの応用が促進される可能性を秘めている。

訳者:津島 悟
ドイツ ヘルムホルツセンター ドレスデン=ロッセンドルフ(HZDR)上席研究員。東京科学大学総合研究院特任准教授兼務
1994年東京大学工学部旧原子力工学科卒業。1999年同博士課程修了。東京大学助手、名古屋大学助教授を経て2005年にヨーロッパに転出。ストックホルム大学、欧州シンクロトロン放射光施設での勤務を経て2007年より現職。2017年より東京工業大学(現東京科学大学)を兼務。元々の専門は原子力実験化学だが、博士課程在学中から研究の軸足を計算化学にシフトさせ、現在はアクチノイドやランタノイドを含む系の量子化化学計算や分子動力学計算に取り組んでおり、計算対象は核燃料再処理のための抽出剤開発から金属タンパク質まで幅広く及ぶ。